TikZ – 08 – Arcos

Ilustrações de matemática costumam ter não só circunferências, mas também arcos de circunferência: vemos arcos o tempo todo marcando ângulos entre os lados de um polígono, entre retas e segmentos e em teoremas clássicos sobre arcos e circunferências. Neste capítulo, aprenderemos como traçar arcos, realizando a chamada pseudo-espiral áurea:

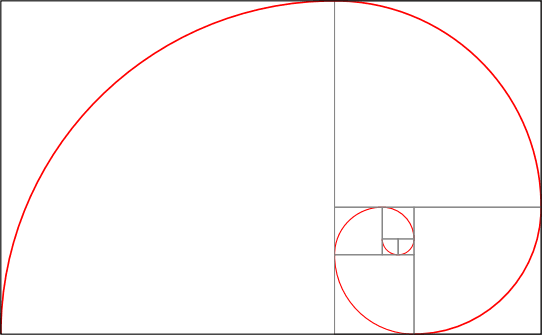
Essa belíssima espiral se relaciona com os chamados números de Fibonacci, de interesse tanto para cientistas quanto para artistas. Antes de desenhá-la, vamos compreender com a TikZ traça arcos.

Arcos

Comecemos com um programa mínimo que gera uma malha muito fina e um pequeno círculo na origem:

\documentclass[tikz]{standalone} 
\begin{document}
  \begin{tikzpicture}
    \draw [gray!20] (-2.1,-2.1) grid (2.1,2.1);
    \filldraw (0,0) circle (0.05);
  \end{tikzpicture}
\end{document}

Esse programa gera a seguinte figura:

A partir de agora, como de costume, vamos apenas mostrar os comando que estão entre \begin{tikzpicture} e \end{tikzpicture}. Não se esqueça disso!

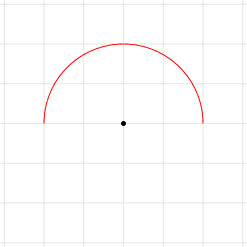
Como a TikZ “enxerga” um arco? Comecemos com um exemplo prático: um arco que começa no ponto (2, 0) e faz um giro de 0° a 180°, com raio 2. Para ressaltar esse arco na figura, vamos traçá-lo com a cor vermelha (red). Logo abaixo da linha que começa com filldraw, acrescente draw [red] (2,0) arc (0:180:2); (sem se esquecer do ponto-e-vírgula):

\draw [gray!20] (-2.1,-2.1) grid (2.1,2.1);
\filldraw (0,0) circle (0.05);
\draw [red] (2,0) arc (0:180:2);

Se tudo deu certo, você deve estar vendo a seguinte figura:

Sim, essa sintaxe vai nos confundir um pouco no começo. Mas isso pode ser superado com alguns exercícios. Por exemplo, tente traçar o seguinte arco, que vai exigir apenas uma ligeira modificação no arco original:

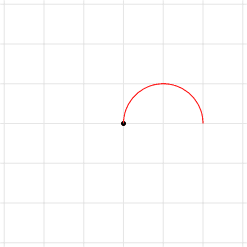
Esse arco, como o anterior, parte de (2, 0) e tem 180°, mas seu raio é 1. Como fica o código? Se você pensou (2,0) arc (0:180:1), você acertou!

Agora, tente desenhar o seguinte arco:

Em verdade, há sempre duas maneiras de traçarmos qualquer arco. Você pode começar de uma extremidade ou de outra. Vamos supor que queremos começar da extremidade de cima, que está no ponto (1, 2) (consegue perceber?). A partir dele, giro de 90 até 270°, com raio 2. Daí, escrevo:

\draw [red] (1,2) arc (90:270:2);

Tente e veja que funciona.

A outra maneira é começar de baixo para cima, do ponto (1, -2) e subir de 270 até 90°:

\draw [red] (1,-2) arc (270:90:2);

Observe que, nesse caso, a TikZ girou no sentido horário!

Você pode usar números negativos nos ângulos, como:

\draw [red] (1,-2) arc (-90:90:2);

Isso forçará a Tikz a seguir o sentido anti-horário, mas o arco desenhado será outro. Tente e veja o que conteceu!

Desenhando a espiral

Vamos, enfim, desenhar a espiral, que vai novamente aqui em toda sua glória:

Pode parecer que teremos um enorme trabalho, mas a coisa é até bem simples: basta notar que temos um só padrão de desenho que se repete, em tamanhos, localizações e rotações diferentes, por toda a espiral: um quadrado com um arco de 90° dentro.

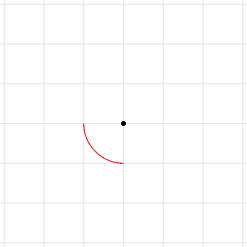
Agora volte à figura 8.2, a malha com a origem. Nela, vamos acrescentar nosso primeiro arco, começando de dentro para fora:

\draw [gray!20] (-2.1,-2.1) grid (2.1,2.1);
\filldraw (0,0) circle (0.05);
\draw [red] (-1,0) arc (180:270:1);

Você deve ter visto isso:

Já aproveitamos e colorimos o arco de vermelho. Agora observe que há um quadrado muito fino ao redor de cada arco. Podemos desenhar esse quadrado usando o que já sabemos sobre traçar segmentos, mas vamos usar um novo comando: rectangle

O comando rectangle

Esse é um comando muito simples, e se parece muito com grid. Nele, você determina dois pontos, um em cada extremo de uma das diagonais do retângulo, e a TikZ traça o retângulo para você.

Por exemplo, o primeiro arco da espiral começa no ponto (-1, 0) e termina no ponto (0, -1). Assim, se você acrescentar a linha

\draw (-1,0) rectangle (0,-1);

logo abaixo da linha que traçou o arco, você terá:

Essa é a peça fundamental do desenho: um arco dentro de um retângulo. O próximo arco é semelhante, e parte do ponto (0, -1) e termina depois de um giro de 270° a 360°, com raio 1. Já vamos acrescentar o retângulo ao redor:

\draw [red] (0,-1) arc (270:360:1);    
\draw (0,-1) rectangle (1,0);

O programa todo, entre begin{tikzpicture} e end{tikzpicture}, é:

\draw [gray!20] (-3.1,-3.1) grid (3.1,3.1);
\filldraw (0,0) circle (0.05);
\draw [red] (-1,0) arc (180:270:1);
\draw (-1,0) rectangle (0,-1);
\draw [red] (0,-1) arc (270:360:1);
\draw (0,-1) rectangle (1,0);

e a imagem gerada deve ser a seguinte:

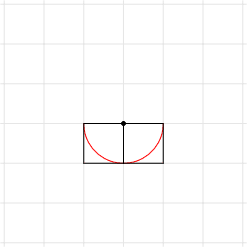
O terceiro arco parte do ponto que o outro terminou, ou seja, (1,0). Agora, o ângulo inicial se torna 0° e o final 90°. Mas o raio aumentou de 1 para 2, ou seja, é a soma dos dois últimos raios. Guarde isso: nessa espiral, o novo raio é a soma dos dois últimos raios!

Com isso em mente, traçamos o arco e quadrado ao redor acrescentando as seguintes linhas ao programa:

\draw [red] (1,0) arc (0:90:2);
\draw (1,0) rectangle (-1,2);

A espiral começa a ganhar corpo:

Como fazer para saber o ponto final do arco? Afinal, precisamos dele para traçar o quadrado. No caso, precisamos saber que o ponto final é (-1, 2). Como fazer? Simples: trace o arco e depois olhe, na grade, onde está seu final. Essa é a maneira mais fácil, visual e intuitiva de descobrir os pontos.

O próximo arco vai extrapolar nossa grade inicial. E o arco depois dele vai extrapolar mais ainda, e assim até o final da espiral. Vamor por parte, aumentando a grade segundo a necessidade. Altere o comando grid para:

\draw [gray!20] (-6.1,-6.1) grid (2.1,2.1);

Isso deve bastar por enquanto. De fato, vamos acrescentar os dois próximos arcos com os comandos:

\draw [red] (-1,2) arc (90:180:3);
\draw (-1,2) rectangle (-4,-1);
\draw [red] (-4,-1) arc (180:270:5);
\draw (-4,-1) rectangle (1,-6);

Observe que o próximo raio, 3, é a soma dos dois últimos raios, ou seja, de 1 e 2. E o raio 5, a soma dos dois últimos raios, ou seja, de 2 e 3, e assim por diante. A figura gerada é:

Os próximos três arcos vão extrapolar novamente a grade e fazer o desenho ficar muito grande. Neste momento, o melhor a fazer é reduzir tudo para uma porcentagem do original. Fazemos isso com o comando scale, já visto em capítulos anteriores (você se lembra dele?), na frente de \begin{tikzpicture}:

\begin{tikzpicture}[scale=0.4]

Isso vai fazer com que a imagem toda seja reduzida a 40% do tamanho original. Agora, podemos novamente alterar a grade, fazendo:

\draw [gray!20] (-25.1,-6.1) grid (9.1,15.1);

Mas de onde vieram essas coordenadas? Tentativa e erro, cara leitora, aumentando aqui e ali, passo a passo, até o fim do programa. Como já fizemos esse processo todo, já testamos e erramos, arrumamos aqui e ali e rejeitamos outras alternativas, resolvemos dar uma ajudinha! E a imagem fica assim:

Você é capaz de continuar a figura, gerando os três últimos arcos? Tente agora, sem olhar para as próximas linhas!

Tentou? Se você fez tudo certo, o código restante é:

\draw [red] (1,-6) arc (270:360:8);
\draw (1,-6) rectangle (9,2);
\draw [red] (9,2) arc (0:90:13);
\draw (9,2) rectangle (-4,15);
\draw [red] (-4,15) arc (90:180:21);
\draw (-25,-6) rectangle (9,15); 

e a figura gerada, quase no final, fica:

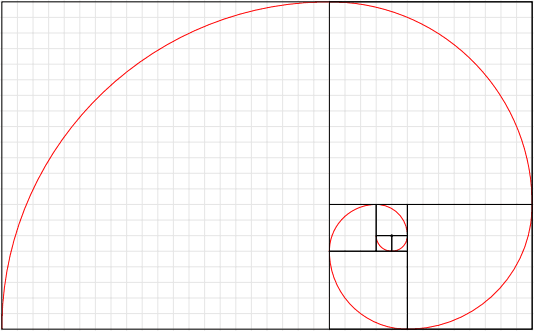
Está quase lá. O mais importante já foi feito. Poderíamos deixar assim, mas vamos fazer alguns ajustes na espessura dos arcos, na cor dos retângulos internos e vamos retirar a malha.

Como essas pequenas alterações são baseadas em gosto e em considerações estéticas pessoais, o que oferecemos como código final acaba sendo uma visão particular do que consideramos mais atraente. Ei-lo aqui, já feitas as modificações decorativas que fizemos:

\documentclass[tikz]{standalone} 
\begin{document}
  \begin{tikzpicture}[scale=0.4]
    \draw [red] (-1,0) arc (180:270:1); 
    \draw [line width=0.01mm, gray] (-1,0) rectangle (0,-1);
    \draw [red] (0,-1) arc (270:360:1);
    \draw [line width=0.01mm, gray] (0,-1) rectangle (1,0);
    \draw [red,thick] (1,0) arc (0:90:2);
    \draw [line width=0.01mm, gray] (1,0) rectangle (-1,2);
    \draw [red,thick] (-1,2) arc (90:180:3);
    \draw [line width=0.01mm, gray] (-1,2) rectangle (-4,-1);
    \draw [red, thick] (-4,-1) arc (180:270:5);
    \draw [line width=0.01mm, gray] (-4,-1) rectangle (1,-6);
    \draw [red,very thick] (1,-6) arc (270:360:8);
    \draw [line width=0.01mm, gray] (1,-6) rectangle (9,2);
    \draw [red,very thick] (9,2) arc (0:90:13);
    \draw [line width=0.01mm, gray] (9,2) rectangle (-4,15);
    \draw [red,very thick] (-4,15) arc (90:180:21);
    \draw [thick] (-25,-6) rectangle (9,15); 
  \end{tikzpicture}
\end{document}

Esse código gera (enfim!) a espiral:

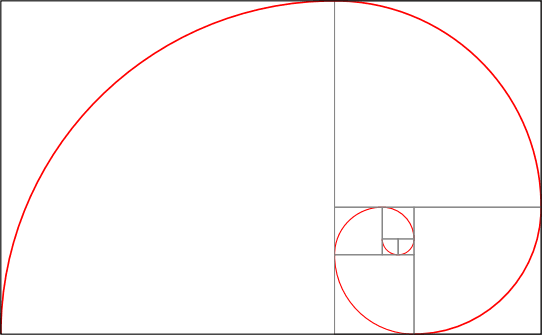
Resumo

Desenho

• (x,y) arc (ini:fim:raio) – define um arco com a seguinte sintaxe: (x, y) define um ponto de uma extremidade do arco; ini define o ângulo inicial a partir do qual o giro do arco começa, e fim, o ângulo onde o giro acaba. O parâmetro raio, obviamente, define o raio do círculo do qual o arco faz parte.
• (a,b) rectangle (c,d) – define um retângulo, onde (a,b) e (c,d) são as extremidades de uma das diagonais. Semelhante a grid.

Decoração

• [thick] e [very thick] – que significam grosso e muito grosso, definem a espessura da linha. Observe que poderíamos ter também [very very thick], ou ainda [very thin] e [very very thin] (muito fino e muito muito fino), em que a palavra very (muito) pode ser usada até duas vezes diante de outra palavra.

Exercícios

• Tente desenhar três arcos concêntricos de 30^o, 45^o e 60^o partindo de (1, 0), (1.5, 0) e (2, 0). Esses arcos podem ser no sentido horário ou anti-horário. Cuidado com os raios!
• Desenhe uma “onda” de 5 arcos de 180^o, com raio 2, um após o outro, comçando em (0,0). Os arcos devem ter concavidades alternadas. Aqui vão os dois primeiros:

\draw (0,0) arc (180:0:2);
\draw (4,0) arc (180:360:2);

DESAFIO!

Você seria capaz de refazer essa espiral, mas espelhada? Ou de cabeça para baixo? Ou ainda, começar de fora para dentro?

Para simplificar os cálculos, você pode usar coordenadas relativas. Lembra-se delas? Não? Tente o seguinte comando, em que os arcos se sucedem um após o outro:

 \draw [red] (-1,0) arc (180:270:1) arc (270:360:1) arc (0:90:2) arc (90:180:3) arc (180:270:5) arc (270:360:8) arc (0:90:13) arc (90:180:21);

Viu? Por que não nos lembramos disso antes?

Coordenadas relativas ajudarão muito no próximo desafio. Antes, observe que nossa espiral deu duas voltas completas ao redor da origem, com quatro arcos de 90°. Mas como seria uma pseudo-espiral áurea que usa 3 arcos de 120° para dar uma volta completa? Esse é seu verdadeiro desafio: desenhe essa espiral de arcos de 120°, mas dê três voltas completas ao redor da origem. E, para completar, ligue as extremidades de cada arco com um segmento de reta azul.